ฟังก์ชันขั้นบันได
ฟังก์ชันขั้นบันได หมายถึง ฟังก์ชันที่มีโดเมนเป็นสับเซตของจำนวนจริง และมีค่าของฟังก์ชันเป็นค่าคงตัวเป็นช่วงๆ มากกว่าสองช่วง กราฟของฟังก์ชันนี้มีลักษณะคล้ายขั้นบัน อ่านต่อ

 f(x) = a(x-h)2 + k , a > 0
f(x) = a(x-h)2 + k , a > 0  f(x) = a(x-h)2 + k , a < 0
f(x) = a(x-h)2 + k , a < 0 

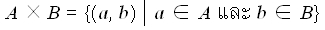



 สามารถแยกได้เป็น
สามารถแยกได้เป็น  เป็นต้นจำนวนเชิงซ้อน (อังกฤษ : complex number) ในทางคณิตศาสตร์ คือ เซตที่ต่อเติมจากเซตของจำนวนจริงโดยเพิ่มจำนวน
เป็นต้นจำนวนเชิงซ้อน (อังกฤษ : complex number) ในทางคณิตศาสตร์ คือ เซตที่ต่อเติมจากเซตของจำนวนจริงโดยเพิ่มจำนวน  ซึ่งทำให้สมการ
ซึ่งทำให้สมการ  เป็นจริง และหลังจากนั้นเพิ่มสมาชิกตัวอื่น ๆ เข้าไปจนกระทั่งเซตที่ได้ใหม่มีสมบัติการปิดภายใต้การบวกและการคูณ จำนวนเชิงซ้อน
เป็นจริง และหลังจากนั้นเพิ่มสมาชิกตัวอื่น ๆ เข้าไปจนกระทั่งเซตที่ได้ใหม่มีสมบัติการปิดภายใต้การบวกและการคูณ จำนวนเชิงซ้อน  ทุกตัวสามารถเขียนอยู่ในรูป
ทุกตัวสามารถเขียนอยู่ในรูป  โดยที่
โดยที่  และ
และ  เป็นจำนวนจริง โดยเราเรียก
เป็นจำนวนจริง โดยเราเรียก  และ
และ  ว่าส่วนจริง (real part) และส่วนจินตภาพ (imaginary part) ของ
ว่าส่วนจริง (real part) และส่วนจินตภาพ (imaginary part) ของ  ตามลำดับ
ตามลำดับ